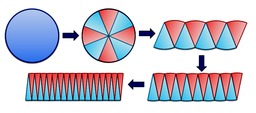
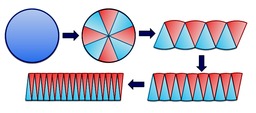
Recently someone posted an animation of a way to visualise the
area of a circle. It was on Twitter, so I can’t find it again,
but here at right is an image taken from http://mathandmultimedia.com/

Someone asked if there was a similar visualisation of the volume
of a sphere, or the surface area of a sphere, and that started me
thinking.

We know that for a circle, for some reason, the circumference is
the derivative of the area, and similarly for the sphere, the
surface area is the derivative of the volume, and I wondering
about visualisations of that, and related things. This is what
I came up with – I’d welcome comment, thoughts, and feedback.

We start with a unit cube.

Consider one vertex of the cube, which is adjacent to three faces.

For each of the other three faces, we have a square-based
pyramid with the face as the base, and the chosen vertex as the
apex. There are several ways to see that, and to be honest, the
absolute best is to make a model for yourself.

However, in lieu of that, here’s a picture:

Each of the three faces gives one of these square-based pyramids, so
the cube is made of three identical skew square-based pyramids.

You can play with an interactive version of that here:

• 
  Trisecting the cube into pyramids
  
  
  (opens in a new tab or window)
  

Now stand one of the pyramids on its base, and think of it as being a
collection of horizontal slices. Those slices can be slid sideways, so
the apex can be dragged around, parallel to the base, and the volume
will remain unchanged.

This is called “Cavalieri’s principle” and you can play with an
interactive version of that here:

• 
  Cavalieri’s Principle
  
  
  (opens in a new tab or window)
  

So we can convert our non-right pyramid into a square-based right
pyramid.

Thus we’ve shown that a square-based pyramid of base area 1 and height
1 has a volume of $1/3$.

We can scale or transform each slice. If we choose a new shape, we can
convert each square slice into that new shape, and provided the area of
the slice remains the same, we don’t change the volume.

Similarly, we can scale each slice, and the volume changes by the same
scale.

So for example, replace each square with a disk of the same area. The
result is then a cone with the same volume. Now scale each disk down to
half the area. The result is still a cone, but now with half the volume.
We have halved the area of the base, so we have halved the volume of the
cone. This shows that the volume is still $1/3$ times the height (which
is still 1) times the area of the base.

Finally, consider the height. If we scale vertically then we change the
volume by the scaling factor. Consider doubling the number of slices.
In doing so we double the height, and double the volume.

Alternatively, if we want to finish with height $h$ then start with a cube
of size $h^3$. Then the area of the base of the square-based pyramid is
$h^2$ and everything follows. I’ll leave it to the (mythical) interested
reader to work through the details, but it’s all there.

So we finally have the general formula that:

• The volume of a cone is $1/3$ times the height times the area of the base.

So that’s nice.

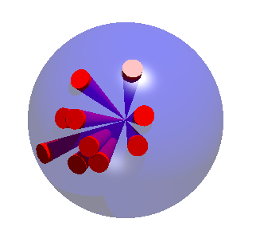
And now a piece of magic occurs …

Consider a sphere of radius $r$, and divide the surface into many,
many small patches. Each small patch induces a “cone” to the centre,
and each of those cones has a volume of $1/3$ times the radius times
the area of the patch.

So the total volume of the sphere is $1/3$ times $r$ times the total
of the areas of the patches. But the total of the areas of the patches
is the surface area of the sphere. So if the surface area of the sphere
is $S$, then the volume of the sphere is $1/3$ times $r$ times $S$.

Now we need the surface of the sphere. That is given to us by the
Archimedes Hat Box Theorem (see the box on the right), and is
$4{pi}r^2.$

So the volume of a sphere of radius $r$ is $frac{4}{3}{pi}r^3$.

Another observation

If the surface area of a sphere is $4{pi}r^2$ then when we increase
the radius by a tiny amount, $dr$, the volume increases by the volume
of the “egg shell” created, which is $4{pi}r^2.dr$. We can then get
the volume of the sphere by taking lots and lots of “egg-shells”, and
we represent this as the integral $0$ to $r$ of $(4{pi}r^2).dr$

So the volume is $int_0^r 4{pi}x^2.dx$ which we’ve seen to be
$frac{4}{3}{pi}r^3$. Dividing through by $4pi$ we therefore see
that $int_0^1 x^2 dx = 1/3$.

We should be able to apply this “growing egg shell” argument to other
shapes – the most obvious to try is the cube. Consider a cube of
“radius” $r$, hence “diameter” $2r$, hence volume $(2r)^3=8r^3$.

A small increase $dr$ in “radius” leads to an increase in volume of
$6(2r)^2.dr$ (six faces, each of size $2r$ by $2r$ and thickness $dr$).
So the volume is $int_0^r 6(2r)^2 dr$ which is $int_0^r 24r^2 dr$.
This evaluates to $24(1/3)r^3 = 8r^3$, just as above.

So the technique works for the cube as well.

For extra credit …

Anyone for the volume of a tetrahedron?

My thanks to …

… Philipp Reinhard,
Robert Low,
[email protected],
Andrea Della Corte,
and others to be included when (or if!) they give their permission, for reading
and commenting on earlier versions of this post.

Send us a comment …

Leave a Reply Cancel reply

document.addEventListener(‘DOMContentLoaded’, function () {
var commentForms = document.getElementsByClassName(‘jetpack_remote_comment’);
for (var i = 0; i < commentForms.length; i++) {
commentForms[i].allowTransparency = false;
commentForms.scrolling = 'no';
}
});
<!–